Classes
struct	AddableConcept

class	angle_cmp

class	BaseIterator

class	Bezier

class	BezierCurve

class	BezierCurve< 0 >

class	Circulator

struct	ContainmentOrder

class	ContinuityError

class	ConvexHull

struct	Crosser

struct	Crossing

struct	CrossingNode

struct	CrossingOrder

class	Curve

struct	CurveHelpers

class	D2

class	DuplicatingIterator

struct	Edge

class	Eigen

class	EllipticalArc

struct	Event

class	Exception

struct	FragmentConcept

class	Hat

class	Interval

class	InvariantsViolation

class	IPoint

class	Linear

class	Linear2d

class	LogicalError

class	Matrix

struct	MonoCrosser

struct	MultiplicableConcept

struct	NearConcept

class	NotImplemented

class	NotInvertible

struct	OffsetableConcept

class	OldBezier

class	Path

class	PathBuilder

class	Piecewise

class	Point
	Cartesian point. More...

class	RangeError

class	Region

struct	ResultTraits

struct	ResultTraits< double >

struct	ResultTraits< Point >

class	Rotate

class	SBasis

class	SBasis2d

class	SBasisCurve

struct	ScalableConcept

class	Scale

class	Shape

struct	SimpleCrosser

class	sturm

class	SVGEllipticalArc

class	SVGPathGenerator

struct	SVGPathParseError

class	SVGPathSink

struct	TimeOrder

struct	TransformConcept

class	Translate

class	Tri

Typedefs
typedef Point	BezierCurve[]

typedef double	Coord

typedef std::vector< Crossing >	Crossings

typedef std::vector< CrossingNode >	CrossingGraph

typedef std::vector< Crossings >	CrossingSet

typedef SimpleCrosser	DefaultCrosser

typedef BezierCurve< 1 >	LineSegment

typedef BezierCurve< 2 >	QuadraticBezier

typedef BezierCurve< 3 >	CubicBezier

typedef long	ICoord

typedef std::vector< Region >	Regions

typedef std::back_insert_iterator< std::vector< Path > >	iter

Enumerations
enum	IntersectorKind { intersects = 0, parallel, coincident, no_intersection }

enum	Dim2 { X =0, Y =1 }

enum	{ BOOLOP_JUST_A = 1, BOOLOP_JUST_B = 2, BOOLOP_BOTH = 4, BOOLOP_NEITHER = 8 }

enum	{ BOOLOP_NULL = 0, BOOLOP_INTERSECT = BOOLOP_BOTH, BOOLOP_SUBTRACT_A_B = BOOLOP_JUST_B, BOOLOP_IDENTITY_A = BOOLOP_JUST_A \| BOOLOP_BOTH, BOOLOP_SUBTRACT_B_A = BOOLOP_JUST_A, BOOLOP_IDENTITY_B = BOOLOP_JUST_B \| BOOLOP_BOTH, BOOLOP_EXCLUSION = BOOLOP_JUST_A \| BOOLOP_JUST_B, BOOLOP_UNION = BOOLOP_JUST_A \| BOOLOP_JUST_B \| BOOLOP_BOTH }

Functions
double	deg_to_rad (double deg)

double	rad_to_deg (double rad)

std::vector< std::pair< double, double > >	find_intersections (vector< Geom::Point > const &A, vector< Geom::Point > const &B)

std::vector< std::pair< double, double > >	find_self_intersections (OldBezier const &Sb)

std::vector< std::pair< double, double > >	find_self_intersections (D2< SBasis > const &A)

bool	intersect_BB (OldBezier a, OldBezier b)

void	recursively_intersect (OldBezier a, double t0, double t1, int deptha, OldBezier b, double u0, double u1, int depthb, std::vector< std::pair< double, double > > &parameters)

double	log4 (double x)

double	Lmax (Point p)

unsigned	wangs_theorem (OldBezier a)

std::vector< std::pair< double, double > >	find_intersections (D2< SBasis > const &A, D2< SBasis > const &B)

std::vector< std::pair< double, double > >	find_intersections (std::vector< Point > const &A, std::vector< Point > const &B)

std::vector< std::pair< double, double > >	find_self_intersections (std::vector< Point > const &A)

SBasis	bezier_to_sbasis (Coord const *handles, unsigned order)

template<typename T >
D2< SBasis >	handles_to_sbasis (T const &handles, unsigned order)

int	bezier_fit_cubic (Point bezier, Point const data, int len, double error)

int	bezier_fit_cubic_r (Point bezier[], Point const data[], int const len, double const error, unsigned const max_beziers)

int	bezier_fit_cubic_full (Point bezier[], int split_points[], Point const data[], int const len, Point const &tHat1, Point const &tHat2, double const error, unsigned const max_beziers)

Point	bezier_pt (unsigned const degree, Point const V[], double const t)

Point	darray_left_tangent (Point const d[], unsigned const len)

Point	darray_left_tangent (Point const d[], unsigned const len, double const tolerance_sq)

Point	darray_right_tangent (Point const d[], unsigned const len, double const tolerance_sq)

int	bezier_fit_cubic (Point bezier[], Point const data[], int len, double error)

Coord	subdivideArr (Coord t, Coord const v, Coord left, Coord *right, unsigned order)

Bezier	operator+ (const Bezier &a, double v)

Bezier	operator- (const Bezier &a, double v)

Bezier	operator* (const Bezier &a, double v)

Bezier	operator/ (const Bezier &a, double v)

Bezier	reverse (const Bezier &a)

Bezier	portion (const Bezier &a, double from, double to)

std::vector< Point >	bezier_points (const D2< Bezier > &a)

Bezier	derivative (const Bezier &a)

Bezier	integral (const Bezier &a)

Interval	bounds_fast (Bezier const &b)

Interval	bounds_exact (Bezier const &b)

Interval	bounds_local (Bezier const &b, Interval i)

std::ostream &	operator<< (std::ostream &out_file, const Bezier &b)

int	circle_circle_intersection (Point X0, double r0, Point X1, double r1, Point &p0, Point &p1)

template<typename T >
T	portion (const T &t, const Interval &i)

double	SignedTriangleArea (Point p0, Point p1, Point p2)

int	mod (int i, int l)

pair< map< int, int >, map< int, int > >	bridges (ConvexHull a, ConvexHull b)

std::vector< Point >	bridge_points (ConvexHull a, ConvexHull b)

unsigned	find_bottom_right (ConvexHull const &a)

ConvexHull	sweepline_intersection (ConvexHull const &a, ConvexHull const &b)

ConvexHull	intersection (ConvexHull a, ConvexHull b)

ConvexHull	merge (ConvexHull a, ConvexHull b)

ConvexHull	graham_merge (ConvexHull a, ConvexHull b)

bool	intersectp (ConvexHull a, ConvexHull b)

template<class T >
ConvexHull	operator* (ConvexHull const &p, T const &m)

bool	are_near (Coord a, Coord b, double eps=EPSILON)

double	wrap_dist (double from, double to, double size, bool rev)

CrossingGraph	create_crossing_graph (std::vector< Path > const &p, Crossings const &crs)

void	merge_crossings (Crossings &a, Crossings &b, unsigned i)

void	offset_crossings (Crossings &cr, double a, double b)

Crossings	reverse_ta (Crossings const &cr, std::vector< double > max)

Crossings	reverse_tb (Crossings const &cr, unsigned split, std::vector< double > max)

CrossingSet	reverse_ta (CrossingSet const &cr, unsigned split, std::vector< double > max)

CrossingSet	reverse_tb (CrossingSet const &cr, unsigned split, std::vector< double > max)

void	clean (Crossings &cr_a, Crossings &cr_b)

template<typename C >
std::vector< Rect >	bounds (C const &a)

void	sort_crossings (Crossings &cr, unsigned ix)

SBasis	L2 (D2< SBasis > const &a, unsigned k)

D2< SBasis >	multiply (Linear const &a, D2< SBasis > const &b)

D2< SBasis >	multiply (SBasis const &a, D2< SBasis > const &b)

D2< SBasis >	truncate (D2< SBasis > const &a, unsigned terms)

unsigned	sbasis_size (D2< SBasis > const &a)

double	tail_error (D2< SBasis > const &a, unsigned tail)

Piecewise< D2< SBasis > >	sectionize (D2< Piecewise< SBasis > > const &a)

D2< Piecewise< SBasis > >	make_cuts_independant (Piecewise< D2< SBasis > > const &a)

Piecewise< D2< SBasis > >	rot90 (Piecewise< D2< SBasis > > const &M)

Piecewise< SBasis >	dot (Piecewise< D2< SBasis > > const &a, Piecewise< D2< SBasis > > const &b)

Piecewise< SBasis >	cross (Piecewise< D2< SBasis > > const &a, Piecewise< D2< SBasis > > const &b)

Piecewise< D2< SBasis > >	operator* (Piecewise< D2< SBasis > > const &a, Matrix const &m)

Piecewise< D2< SBasis > >	force_continuity (Piecewise< D2< SBasis > > const &f, double tol, bool closed)

template<typename T >
D2< T >	reverse (const D2< T > &a)

template<typename T >
D2< T >	portion (const D2< T > &a, Coord f, Coord t)

template<typename T >
bool	operator== (D2< T > const &a, D2< T > const &b)

template<typename T >
bool	operator!= (D2< T > const &a, D2< T > const &b)

template<typename T >
bool	are_near (D2< T > const &a, D2< T > const &b, double tol)

template<typename T >
D2< T >	operator+ (D2< T > const &a, D2< T > const &b)

template<typename T >
D2< T >	operator- (D2< T > const &a, D2< T > const &b)

template<typename T >
D2< T >	operator+= (D2< T > &a, D2< T > const &b)

template<typename T >
D2< T >	operator-= (D2< T > &a, D2< T > const &b)

template<typename T >
D2< T >	operator- (D2< T > const &a)

template<typename T >
D2< T >	operator* (D2< T > const &a, Point const &b)

template<typename T >
D2< T >	operator/ (D2< T > const &a, Point const &b)

template<typename T >
D2< T >	*operator=** (D2< T > &a, Point const &b)

template<typename T >
D2< T >	operator/= (D2< T > &a, Point const &b)

template<typename T >
D2< T >	operator* (D2< T > const &a, double b)

template<typename T >
D2< T >	*operator=** (D2< T > &a, double b)

template<typename T >
D2< T >	operator/ (D2< T > const &a, double b)

template<typename T >
D2< T >	operator/= (D2< T > &a, double b)

template<typename T >
D2< T >	operator* (D2< T > const &v, Matrix const &m)

template<typename T >
D2< T >	operator+ (D2< T > const &a, Point b)

template<typename T >
D2< T >	operator- (D2< T > const &a, Point b)

template<typename T >
D2< T >	operator+= (D2< T > &a, Point b)

template<typename T >
D2< T >	operator-= (D2< T > &a, Point b)

template<typename T >
T	dot (D2< T > const &a, D2< T > const &b)

template<typename T >
T	cross (D2< T > const &a, D2< T > const &b)

template<typename T >
D2< T >	rot90 (D2< T > const &a)

template<typename T >
D2< T >	compose (D2< T > const &a, T const &b)

template<typename T >
D2< T >	compose_each (D2< T > const &a, D2< T > const &b)

template<typename T >
D2< T >	compose_each (T const &a, D2< T > const &b)

template<typename T >
D2< T >	derivative (D2< T > const &a)

template<typename T >
D2< T >	integral (D2< T > const &a)

template<typename T >
Rect	bounds_fast (const D2< T > &a)

template<typename T >
Rect	bounds_exact (const D2< T > &a)

template<typename T >
Rect	bounds_local (const D2< T > &a, const Interval &t)

IntersectorKind	line_intersection (Geom::Point const &n0, double const d0, Geom::Point const &n1, double const d1, Geom::Point &result)

int	intersector_ccw (const Geom::Point &p0, const Geom::Point &p1, const Geom::Point &p2)

IntersectorKind	segment_intersect (Geom::Point const &p00, Geom::Point const &p01, Geom::Point const &p10, Geom::Point const &p11, Geom::Point &result)

IntersectorKind	line_twopoint_intersect (Geom::Point const &p00, Geom::Point const &p01, Geom::Point const &p10, Geom::Point const &p11, Geom::Point &result)

int	centroid (std::vector< Geom::Point > p, Geom::Point &centroid, double &area)

Interval	operator+ (const Interval &a, const Interval &b)

Interval	operator- (const Interval &a, const Interval &b)

Interval	operator+= (Interval &a, const Interval &b)

Interval	operator-= (Interval &a, const Interval &b)

Interval	operator* (const Interval &a, const Interval &b)

Interval	*operator=** (Interval &a, const Interval &b)

Interval	unify (const Interval &a, const Interval &b)

boost::optional< Interval >	intersect (const Interval &a, const Interval &b)

double	lerp (double t, double a, double b)

Linear	reverse (Linear const &a)

Linear	operator+ (Linear const &a, Linear const &b)

Linear	operator- (Linear const &a, Linear const &b)

Linear &	operator+= (Linear &a, Linear const &b)

Linear &	operator-= (Linear &a, Linear const &b)

Linear	operator+ (Linear const &a, double b)

Linear	operator- (Linear const &a, double b)

Linear &	operator+= (Linear &a, double b)

Linear &	operator-= (Linear &a, double b)

bool	operator== (Linear const &a, Linear const &b)

bool	operator!= (Linear const &a, Linear const &b)

Linear	operator- (Linear const &a)

Linear	operator* (Linear const &a, double b)

Linear	operator/ (Linear const &a, double b)

Linear	*operator=** (Linear &a, double b)

Linear	operator/= (Linear &a, double b)

Matrix	from_basis (Point const x_basis, Point const y_basis, Point const offset)

Matrix	operator* (Matrix const &m0, Matrix const &m1)

Matrix	elliptic_quadratic_form (Matrix const &m)

std::ostream &	operator<< (std::ostream &out_file, const Geom::Matrix &m)

Matrix	identity ()

bool	operator== (Matrix const &a, Matrix const &b)

bool	operator!= (Matrix const &a, Matrix const &b)

int	winding (Path const &path, Point p)

bool	path_direction (Path const &p)

template<typename T >
void	append (T &a, T const &b)

bool	linear_intersect (Point A0, Point A1, Point B0, Point B1, double &tA, double &tB, double &det)

void	pair_intersect (Curve const &A, double Al, double Ah, Curve const &B, double Bl, double Bh, Crossings &ret, unsigned depth=0)

void	mono_pair (Path const &A, double Al, double Ah, Path const &B, double Bl, double Bh, Crossings &ret, double tol, unsigned depth=0)

std::vector< double >	curve_mono_splits (Curve const &d)

std::vector< double >	offset_doubles (std::vector< double > const &x, double offs)

std::vector< double >	path_mono_splits (Path const &p)

std::vector< std::vector< double > >	paths_mono_splits (std::vector< Path > const &ps)

std::vector< std::vector< Rect > >	split_bounds (std::vector< Path > const &p, std::vector< std::vector< double > > splits)

Crossings	curve_self_crossings (Curve const &a)

Crossings	self_crossings (Path const &p)

void	flip_crossings (Crossings &crs)

CrossingSet	crossings_among (std::vector< Path > const &p)

bool	contains (Path const &p, Point i, bool evenodd=true)

template<typename T >
Crossings	curve_sweep (Path const &a, Path const &b)

Crossings	crossings (Path const &a, Path const &b)

CrossingSet	crossings (std::vector< Path > const &a, std::vector< Path > const &b)

template<typename iter >
iter	inc (iter const &x, unsigned n)

Piecewise< SBasis >	divide (Piecewise< SBasis > const &a, Piecewise< SBasis > const &b, unsigned k)

Piecewise< SBasis >	divide (Piecewise< SBasis > const &a, Piecewise< SBasis > const &b, double tol, unsigned k, double zero)

Piecewise< SBasis >	divide (Piecewise< SBasis > const &a, SBasis const &b, double tol, unsigned k, double zero)

Piecewise< SBasis >	divide (SBasis const &a, Piecewise< SBasis > const &b, double tol, unsigned k, double zero)

Piecewise< SBasis >	divide (SBasis const &a, SBasis const &b, double tol, unsigned k, double zero)

std::map< double, unsigned >	compose_pullback (std::vector< double > const &values, SBasis const &g)

int	compose_findSegIdx (std::map< double, unsigned >::iterator const &cut, std::map< double, unsigned >::iterator const &next, std::vector< double > const &levels, SBasis const &g)

std::vector< double >	roots (Piecewise< SBasis > const &f)

template<typename T >
FragmentConcept< T >::BoundsType	bounds_fast (const Piecewise< T > &f)

template<typename T >
FragmentConcept< T >::BoundsType	bounds_exact (const Piecewise< T > &f)

template<typename T >
FragmentConcept< T >::BoundsType	bounds_local (const Piecewise< T > &f, const Interval &m)

template<typename T >
T	elem_portion (const Piecewise< T > &a, unsigned i, double from, double to)

template<typename T >
Piecewise< T >	partition (const Piecewise< T > &pw, std::vector< double > const &c)

template<typename T >
Piecewise< T >	portion (const Piecewise< T > &pw, double from, double to)

template<typename T >
Piecewise< T >	remove_short_cuts (Piecewise< T > const &f, double tol)

template<typename T >
Piecewise< T >	remove_short_cuts_extending (Piecewise< T > const &f, double tol)

template<typename T >
std::vector< double >	roots (const Piecewise< T > &pw)

template<typename T >
Piecewise< T >	operator+ (Piecewise< T > const &a, typename T::output_type b)

template<typename T >
Piecewise< T >	operator- (Piecewise< T > const &a, typename T::output_type b)

template<typename T >
Piecewise< T >	operator+= (Piecewise< T > &a, typename T::output_type b)

template<typename T >
Piecewise< T >	operator-= (Piecewise< T > &a, typename T::output_type b)

template<typename T >
Piecewise< T >	operator- (Piecewise< T > const &a)

template<typename T >
Piecewise< T >	operator* (Piecewise< T > const &a, double b)

template<typename T >
Piecewise< T >	operator/ (Piecewise< T > const &a, double b)

template<typename T >
Piecewise< T >	*operator=** (Piecewise< T > &a, double b)

template<typename T >
Piecewise< T >	operator/= (Piecewise< T > &a, double b)

template<typename T >
Piecewise< T >	operator+ (Piecewise< T > const &a, Piecewise< T > const &b)

template<typename T >
Piecewise< T >	operator- (Piecewise< T > const &a, Piecewise< T > const &b)

template<typename T >
Piecewise< T >	operator+= (Piecewise< T > &a, Piecewise< T > const &b)

template<typename T >
Piecewise< T >	operator-= (Piecewise< T > &a, Piecewise< T > const &b)

template<typename T1 , typename T2 >
Piecewise< T2 >	operator* (Piecewise< T1 > const &a, Piecewise< T2 > const &b)

template<typename T >
Piecewise< T >	*operator=** (Piecewise< T > &a, Piecewise< T > const &b)

template<typename T >
Piecewise< T >	compose (Piecewise< T > const &f, SBasis const &g)

template<typename T >
Piecewise< T >	compose (Piecewise< T > const &f, Piecewise< SBasis > const &g)

template<typename T >
Piecewise< T >	integral (Piecewise< T > const &a)

template<typename T >
Piecewise< T >	derivative (Piecewise< T > const &a)

Coord	L1 (Point const &p)

Coord	LInfty (Point const &p)

bool	is_zero (Point const &p)

bool	is_unit_vector (Point const &p)

Coord	atan2 (Point const p)

Coord	angle_between (Point const a, Point const b)

Point	unit_vector (Point const &a)

Point	abs (Point const &b)

Point	operator* (Point const &v, Matrix const &m)

Point	operator/ (Point const &p, Matrix const &m)

Point	operator* (double const s, Point const &p)

std::ostream &	operator<< (std::ostream &out_file, const Geom::Point &in_pnt)

Point	operator^ (Point const &a, Point const &b)

bool	operator== (Point const &a, Point const &b)

bool	operator!= (Point const &a, Point const &b)

bool	operator<= (Point const &a, Point const &b)

Coord	L2 (Point const &p)

Coord	L2sq (Point const &p)

bool	are_near (Point const &a, Point const &b, double const eps=EPSILON)

Point	rot90 (Point const &p)

Point	lerp (double const t, Point const a, Point const b)

Coord	dot (Point const &a, Point const &b)

Coord	cross (Point const &a, Point const &b)

Coord	distance (Point const &a, Point const &b)

Coord	distanceSq (Point const &a, Point const &b)

unsigned	outer_index (Regions const &ps)

Regions	regions_from_paths (std::vector< Path > const &ps)

std::vector< Path >	paths_from_regions (Regions const &rs)

Regions	sanitize_path (Path const &p)

Regions	region_boolean (bool rev, Region const &a, Region const &b, Crossings const &cr)

Regions	region_boolean (bool rev, Region const &a, Region const &b, Crossings const &cr_a, Crossings const &cr_b)

Regions	region_boolean (bool rev, Region const &a, Region const &b)

SBasis	extract_u (SBasis2d const &a, double u)

SBasis	extract_v (SBasis2d const &a, double v)

SBasis	compose (Linear2d const &a, D2< SBasis > const &p)

SBasis	compose (SBasis2d const &fg, D2< SBasis > const &p)

D2< SBasis >	compose_each (D2< SBasis2d > const &fg, D2< SBasis > const &p)

Linear	extract_u (Linear2d const &a, double u)

Linear	extract_v (Linear2d const &a, double v)

Linear2d	operator- (Linear2d const &a)

Linear2d	operator+ (Linear2d const &a, Linear2d const &b)

Linear2d	operator- (Linear2d const &a, Linear2d const &b)

Linear2d &	operator+= (Linear2d &a, Linear2d const &b)

Linear2d &	operator-= (Linear2d &a, Linear2d const &b)

Linear2d &	*operator=** (Linear2d &a, double b)

bool	operator== (Linear2d const &a, Linear2d const &b)

bool	operator!= (Linear2d const &a, Linear2d const &b)

Linear2d	operator* (double const a, Linear2d const &b)

SBasis2d	operator- (const SBasis2d &p)

SBasis2d	operator+ (const SBasis2d &a, const SBasis2d &b)

SBasis2d	operator- (const SBasis2d &a, const SBasis2d &b)

SBasis2d &	operator+= (SBasis2d &a, const Linear2d &b)

SBasis2d &	operator-= (SBasis2d &a, const Linear2d &b)

SBasis2d &	operator+= (SBasis2d &a, double b)

SBasis2d &	operator-= (SBasis2d &a, double b)

SBasis2d &	*operator=** (SBasis2d &a, double b)

SBasis2d &	operator/= (SBasis2d &a, double b)

SBasis2d	operator* (double k, SBasis2d const &a)

SBasis2d	operator* (SBasis2d const &a, SBasis2d const &b)

SBasis2d	shift (SBasis2d const &a, int sh)

SBasis2d	shift (Linear2d const &a, int sh)

SBasis2d	truncate (SBasis2d const &a, unsigned terms)

SBasis2d	multiply (SBasis2d const &a, SBasis2d const &b)

SBasis2d	integral (SBasis2d const &c)

SBasis2d	derivative (SBasis2d const &a)

SBasis2d	sqrt (SBasis2d const &a, int k)

SBasis2d	reciprocal (Linear2d const &a, int k)

SBasis2d	divide (SBasis2d const &a, SBasis2d const &b, int k)

SBasis2d	compose (SBasis2d const &a, SBasis2d const &b)

SBasis2d	compose (SBasis2d const &a, SBasis2d const &b, unsigned k)

SBasis2d	inverse (SBasis2d const &a, int k)

std::ostream &	operator<< (std::ostream &out_file, const Linear2d &bo)

std::ostream &	operator<< (std::ostream &out_file, const SBasis2d &p)

Piecewise< D2< SBasis > >	cutAtRoots (Piecewise< D2< SBasis > > const &M, double tol=1e-4)

Piecewise< SBasis >	atan2 (D2< SBasis > const &vect, double tol=.01, unsigned order=3)

Piecewise< SBasis >	atan2 (Piecewise< D2< SBasis > >const &vect, double tol=.01, unsigned order=3)

Piecewise< D2< SBasis > >	unitVector (D2< SBasis > const &vect, double tol=.01, unsigned order=3)

Piecewise< D2< SBasis > >	unitVector (Piecewise< D2< SBasis > > const &vect, double tol=.01, unsigned order=3)

Piecewise< SBasis >	curvature (D2< SBasis > const &M, double tol=.01)

Piecewise< SBasis >	curvature (Piecewise< D2< SBasis > > const &M, double tol=.01)

Piecewise< SBasis >	arcLengthSb (D2< SBasis > const &M, double tol=.01)

Piecewise< SBasis >	arcLengthSb (Piecewise< D2< SBasis > > const &M, double tol=.01)

double	length (D2< SBasis > const &M, double tol=.01)

double	length (Piecewise< D2< SBasis > > const &M, double tol=.01)

Piecewise< D2< SBasis > >	arc_length_parametrization (D2< SBasis > const &M, unsigned order=3, double tol=.01)

Piecewise< D2< SBasis > >	arc_length_parametrization (Piecewise< D2< SBasis > > const &M, unsigned order=3, double tol=.01)

unsigned	centroid (Piecewise< D2< SBasis > > const &p, Point &centroid, double &area)

Piecewise< SBasis >	abs (SBasis const &f)

Piecewise< SBasis >	abs (Piecewise< SBasis > const &f)

Piecewise< SBasis >	max (SBasis const &f, SBasis const &g)

Piecewise< SBasis >	max (Piecewise< SBasis > const &f, SBasis const &g)

Piecewise< SBasis >	max (SBasis const &f, Piecewise< SBasis > const &g)

Piecewise< SBasis >	max (Piecewise< SBasis > const &f, Piecewise< SBasis > const &g)

Piecewise< SBasis >	min (SBasis const &f, SBasis const &g)

Piecewise< SBasis >	min (Piecewise< SBasis > const &f, SBasis const &g)

Piecewise< SBasis >	min (SBasis const &f, Piecewise< SBasis > const &g)

Piecewise< SBasis >	min (Piecewise< SBasis > const &f, Piecewise< SBasis > const &g)

Piecewise< SBasis >	signSb (SBasis const &f)

Piecewise< SBasis >	signSb (Piecewise< SBasis > const &f)

Piecewise< SBasis >	sqrt (SBasis const &f, double tol, int order)

Piecewise< SBasis >	sqrt (Piecewise< SBasis > const &f, double tol, int order)

Piecewise< SBasis >	sin (SBasis const &f, double tol, int order)

Piecewise< SBasis >	sin (Piecewise< SBasis > const &f, double tol, int order)

Piecewise< SBasis >	cos (Piecewise< SBasis > const &f, double tol, int order)

Piecewise< SBasis >	cos (SBasis const &f, double tol, int order)

void	truncateResult (Piecewise< SBasis > &f, int order)

Piecewise< SBasis >	reciprocalOnDomain (Interval range, double tol)

Piecewise< SBasis >	reciprocal (SBasis const &f, double tol, int order)

Piecewise< SBasis >	reciprocal (Piecewise< SBasis > const &f, double tol, int order)

Piecewise< SBasis >	log (SBasis const &f, double tol=1e-3, int order=3)

Piecewise< SBasis >	log (Piecewise< SBasis >const &f, double tol=1e-3, int order=3)

SBasis	poly_to_sbasis (Poly const &p)

Poly	sbasis_to_poly (SBasis const &sb)

Interval	bounds_exact (SBasis const &a)

Interval	bounds_fast (const SBasis &sb, int order)

Interval	bounds_local (const SBasis &sb, const Interval &i, int order)

std::vector< std::vector< double > >	multi_roots (SBasis const &f, std::vector< double > const &levels, double htol, double vtol, double a, double b)

void	subdiv_sbasis (SBasis const &s, std::vector< double > &roots, double left, double right)

std::vector< double >	roots (SBasis const &s)

double	W (unsigned n, unsigned j, unsigned k)

Bezier	sbasis_to_bezier (SBasis const &B, unsigned q)

double	mopi (int i)

SBasis	bezier_to_sbasis (Bezier const &B)

std::vector< Geom::Point >	sbasis_to_bezier (D2< SBasis > const &B, unsigned qq)

void	build_from_sbasis (Geom::PathBuilder &pb, D2< SBasis > const &B, double tol)

Path	path_from_sbasis (D2< SBasis > const &B, double tol)

std::vector< Geom::Path >	path_from_piecewise (Geom::Piecewise< Geom::D2< Geom::SBasis > > const &B, double tol)

SBasis	operator+ (const SBasis &a, const SBasis &b)

SBasis	operator- (const SBasis &a, const SBasis &b)

SBasis &	operator+= (SBasis &a, const SBasis &b)

SBasis &	operator-= (SBasis &a, const SBasis &b)

SBasis	operator* (SBasis const &a, double k)

SBasis &	*operator=** (SBasis &a, double b)

SBasis	shift (SBasis const &a, int sh)

SBasis	shift (Linear const &a, int sh)

SBasis	multiply (SBasis const &a, SBasis const &b)

SBasis	integral (SBasis const &c)

SBasis	derivative (SBasis const &a)

SBasis	sqrt (SBasis const &a, int k)

SBasis	reciprocal (Linear const &a, int k)

SBasis	divide (SBasis const &a, SBasis const &b, int k)

SBasis	compose (SBasis const &a, SBasis const &b)

SBasis	compose (SBasis const &a, SBasis const &b, unsigned k)

SBasis	inverse (SBasis a, int k)

SBasis	sin (Linear b, int k)

SBasis	cos (Linear bo, int k)

SBasis	compose_inverse (SBasis const &f, SBasis const &g, unsigned order, double zero)

SBasis	reverse (SBasis const &a)

SBasis	operator- (const SBasis &p)

SBasis	operator* (double k, SBasis const &a)

SBasis	operator/ (SBasis const &a, double k)

SBasis &	operator/= (SBasis &a, double b)

SBasis	operator+ (const SBasis &a, Linear const &b)

SBasis	operator- (const SBasis &a, Linear const &b)

SBasis &	operator+= (SBasis &a, const Linear &b)

SBasis &	operator-= (SBasis &a, const Linear &b)

SBasis	operator+ (const SBasis &a, double b)

SBasis	operator- (const SBasis &a, double b)

SBasis &	operator+= (SBasis &a, double b)

SBasis &	operator-= (SBasis &a, double b)

SBasis	truncate (SBasis const &a, unsigned terms)

SBasis	operator* (SBasis const &a, SBasis const &b)

SBasis &	*operator=** (SBasis &a, SBasis const &b)

unsigned	valuation (SBasis const &a, double tol=0)

SBasis	portion (const SBasis &t, double from, double to)

std::ostream &	operator<< (std::ostream &out_file, const Linear &bo)

std::ostream &	operator<< (std::ostream &out_file, const SBasis &p)

void	first_false (std::vector< std::vector< bool > > visited, unsigned &i, unsigned &j)

unsigned	find_crossing (Crossings const &cr, Crossing x, unsigned i)

Shape	shape_boolean (bool rev, Shape const &a, Shape const &b, CrossingSet const &crs)

Shape	shape_boolean (bool rev, Shape const &a, Shape const &b)

std::vector< double >	region_sizes (Shape const &a)

Shape	shape_boolean_ra (bool rev, Shape const &a, Shape const &b, CrossingSet const &crs)

Shape	shape_boolean_rb (bool rev, Shape const &a, Shape const &b, CrossingSet const &crs)

Shape	boolop (Shape const &a, Shape const &b, unsigned flags, CrossingSet const &crs)

Shape	boolop (Shape const &a, Shape const &b, unsigned flags)

int	paths_winding (std::vector< Path > const &ps, Point p)

void	add_to_shape (Shape &s, Path const &p, bool fill)

int	inner_winding (Path const &p, std::vector< Path > const &ps)

double	fudgerize (double d, bool rev)

unsigned	pick_coincident (unsigned ix, unsigned jx, bool &rev, std::vector< Path > const &ps, CrossingSet const &crs)

unsigned	crossing_along (double t, unsigned ix, unsigned jx, bool dir, Crossings const &crs)

void	crossing_dual (unsigned &i, unsigned &j, CrossingSet const &crs)

void	outer_crossing (unsigned &ix, unsigned &jx, bool &dir, std::vector< Path > const &ps, CrossingSet const &crs)

std::vector< Path >	inner_sanitize (std::vector< Path > const &ps)

Shape	sanitize (std::vector< Path > const &ps)

Shape	stopgap_cleaner (std::vector< Path > const &ps)

CrossingSet	crossings_between (Shape const &a, Shape const &b)

Shape	boolop (Shape const &, Shape const &, unsigned flags, CrossingSet &)

std::vector< Path >	desanitize (Shape const &s)

void	find_bernstein_roots (double const *w, unsigned degree, std::vector< double > &solutions, unsigned depth, double left_t, double right_t)

unsigned	crossing_count (Geom::Point const *V, unsigned degree)

void	find_parametric_bezier_roots (Geom::Point const *w, unsigned degree, std::vector< double > &solutions, unsigned depth)

unsigned	crossing_count (double const *V, unsigned degree, double left_t, double right_t)

void	output (Curve const &curve, SVGPathSink &sink)

void	output (LineSegment const &curve, SVGPathSink &sink)

void	output (CubicBezier const &curve, SVGPathSink &sink)

void	output (QuadraticBezier const &curve, SVGPathSink &sink)

void	output (SVGEllipticalArc const &curve, SVGPathSink &sink)

template<typename T >
bool	output_as (Curve const &curve, SVGPathSink &sink)

void	output_svg_path (Path &path, SVGPathSink &sink)

std::vector< std::vector< unsigned > >	sweep_bounds (std::vector< Rect > rs)

std::vector< std::vector< unsigned > >	sweep_bounds (std::vector< Rect > a, std::vector< Rect > b)

std::vector< std::vector< unsigned > >	fake_cull (unsigned a, unsigned b)

Matrix	operator* (Translate const &t, Scale const &s)

Matrix	operator* (Translate const &t, Rotate const &r)

Matrix	operator* (Scale const &s, Translate const &t)

Matrix	operator* (Scale const &s, Matrix const &m)

Matrix	operator* (Matrix const &m, Translate const &t)

Matrix	operator* (Matrix const &m, Scale const &s)

Point	operator* (Point const &v, Translate const &t)

Point	operator* (Point const &p, Scale const &s)

Point	operator* (Point const &v, Rotate const &r)

Matrix	operator* (Matrix const &m, Rotate const &r)

bool	logical_xor (bool a, bool b)

template<class T >
int	sgn (const T &x)

template<class T >
T	sqr (const T &x)

template<class T >
T	cube (const T &x)

template<class T >
const T &	between (const T &min, const T &max, const T &x)

double	round (double const x)

double	decimal_round (double const x, int const places)

Variables
const double	INV_EPS = (1L<<14)

const Coord	EPSILON = 1e-5

const double	eps = .1

const unsigned	MAXDEPTH = 64

const double	BEPSILON = ldexp(1.0,((signed)-1)-MAXDEPTH)

unsigned	total_steps

unsigned	total_subs

Detailed Description

A convex cover is a sequence of convex polygons that completely cover the path. For now a convex hull class is included here (the convex-hull header is wrong)

Defines the different types of exceptions that 2geom can throw.

This library is free software; you can redistribute it and/or modify it either under the terms of the GNU Lesser General Public License version 2.1 as published by the Free Software Foundation (the "LGPL") or, at your option, under the terms of the Mozilla Public License Version 1.1 (the "MPL"). If you do not alter this notice, a recipient may use your version of this file under either the MPL or the LGPL.

You should have received a copy of the LGPL along with this library in the file COPYING-LGPL-2.1; if not, write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA You should have received a copy of the MPL along with this library in the file COPYING-MPL-1.1

The contents of this file are subject to the Mozilla Public License Version 1.1 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.mozilla.org/MPL/

This software is distributed on an "AS IS" basis, WITHOUT WARRANTY OF ANY KIND, either express or implied. See the LGPL or the MPL for the specific language governing rights and limitations.

These operators are built on a more 'polynomially robust' transformation to map a function that takes a [0,1] parameter to a 2d vector into a function that takes the same [0,1] parameter to a unit vector with the same direction.

Rather that using (X/sqrt(X))(t) which involves two unstable operations, sqrt and divide, this approach forms a curve directly from the various tangent directions at each end (angular jet). As a result, the final path has a convergence behaviour derived from that of the sin and cos series. – njh

Various utility functions.

This library is free software; you can redistribute it and/or modify it either under the terms of the GNU Lesser General Public License version 2.1 as published by the Free Software Foundation (the "LGPL") or, at your option, under the terms of the Mozilla Public License Version 1.1 (the "MPL"). If you do not alter this notice, a recipient may use your version of this file under either the MPL or the LGPL.

You should have received a copy of the LGPL along with this library in the file COPYING-LGPL-2.1; if not, write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA You should have received a copy of the MPL along with this library in the file COPYING-MPL-1.1

The contents of this file are subject to the Mozilla Public License Version 1.1 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.mozilla.org/MPL/

This software is distributed on an "AS IS" basis, WITHOUT WARRANTY OF ANY KIND, either express or implied. See the LGPL or the MPL for the specific language governing rights and limitations.

Typedef Documentation

typedef double Geom::Coord

A "real" type with sufficient precision for coordinates.

You may safely assume that double (or even float) provides enough precision for storing on-canvas points, and hence that double provides enough precision for dot products of differences of on-canvas points.

Function Documentation

double Geom::angle_between	(	Point const	a,
		Point const	b
	)

compute the angle turning from a to b. This should give 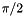$\pi/2$ for angle_between(a, rot90(a)); This works by projecting b onto the basis defined by a, rot90(a)

compute the angle turning from a to b (signed).

template<class T >

const T& Geom::between	(	const T &	min,
		const T &	max,
		const T &	x
	)

inline

Between function - returns true if a number x is within a range. The values delimiting the range and the number must have the same type.

int Geom::bezier_fit_cubic	(	Point *	bezier,
		Point const *	data,
		int	len,
		double	error
	)

Fit a single-segment Bezier curve to a set of digitized points.

Returns: Number of segments generated, or -1 on error.

int Geom::bezier_fit_cubic_full	(	Point	bezier[],
		int	split_points[],
		Point const	data[],
		int const	len,
		Point const &	tHat1,
		Point const &	tHat2,
		double const	error,
		unsigned const	max_beziers
	)

Fit a multi-segment Bezier curve to a set of digitized points, without possible weedout of identical points and NaNs.

Precondition: data is uniqued, i.e. not exist i: data[i] == data[i + 1].

Parameters

max_beziers	Maximum number of generated segments
Result	array, must be large enough for n. segments * 4 elements.

int Geom::bezier_fit_cubic_r	(	Point	bezier[],
		Point const	data[],
		int const	len,
		double const	error,
		unsigned const	max_beziers
	)

Fit a multi-segment Bezier curve to a set of digitized points, with possible weedout of identical points and NaNs.

Parameters

max_beziers	Maximum number of generated segments
Result	array, must be large enough for n. segments * 4 elements.

Returns: Number of segments generated, or -1 on error.

Point Geom::bezier_pt	(	unsigned const	degree,
		Point const	V[],
		double const	t
	)

Evaluate a Bezier curve at parameter value t.

Parameters

degree	The degree of the Bezier curve: 3 for cubic, 2 for quadratic etc. Must be less than 4.
V	The control points for the Bezier curve. Must have (degree+1) elements.
t	The "parameter" value, specifying whereabouts along the curve to evaluate. Typically in the range [0.0, 1.0].

Let s = 1 - t. BezierII(1, V) gives (s, t) * V, i.e. t of the way from V[0] to V[1]. BezierII(2, V) gives (s**2, 2*s*t, t**2) * V. BezierII(3, V) gives (s**3, 3 s**2 t, 3s t**2, t**3) * V.

The derivative of BezierII(i, V) with respect to t is i * BezierII(i-1, V'), where for all j, V'[j] = V[j + 1] - V[j].

Pascal's triangle.

unsigned Geom::centroid	(	Piecewise< D2< SBasis > > const &	p,
		Point &	centroid,
		double &	area
	)

centroid using sbasis integration. This approach uses green's theorem to compute the area and centroid using integrals. For curved shapes this is much faster than converting to polyline.

Returned values: 0 for normal execution; 2 if area is zero, meaning centroid is meaningless.

Copyright Nathan Hurst 2006

int Geom::centroid	(	std::vector< Geom::Point >	p,
		Geom::Point &	centroid,
		double &	area
	)

polyCentroid: Calculates the centroid (xCentroid, yCentroid) and area of a polygon, given its vertices (x[0], y[0]) ... (x[n-1], y[n-1]). It is assumed that the contour is closed, i.e., that the vertex following (x[n-1], y[n-1]) is (x[0], y[0]). The algebraic sign of the area is positive for counterclockwise ordering of vertices in x-y plane; otherwise negative.

Returned values: 0 for normal execution; 1 if the polygon is degenerate (number of vertices < 3); 2 if area = 0 (and the centroid is undefined).

for now we require the path to be a polyline and assume it is closed.

Coord Geom::cross	(	Point const &	a,
		Point const &	b
	)

inline

Defined as dot(a, b.cw()).

Point Geom::darray_left_tangent	(	Point const	d[],
		unsigned const	len
	)

Estimate the (forward) tangent at point d[first + 0.5].

Unlike the center and right versions, this calculates the tangent in the way one might expect, i.e., wrt increasing index into d.

Precondition: (2 <= len) and (d[0] != d[1]).

Point Geom::darray_left_tangent	(	Point const	d[],
		unsigned const	len,
		double const	tolerance_sq
	)

Estimate the (forward) tangent at point d[0].

Unlike the center and right versions, this calculates the tangent in the way one might expect, i.e., wrt increasing index into d.

Precondition: 2 <= len.; d[0] != d[1].; all[p in d] in_svg_plane(p).

Postcondition: is_unit_vector(ret).

Point Geom::darray_right_tangent	(	Point const	d[],
		unsigned const	len,
		double const	tolerance_sq
	)

Estimates the (backward) tangent at d[last].

Note: The tangent is "backwards", i.e. it is with respect to decreasing index rather than increasing index.

Precondition: 2 <= len.; d[len - 1] != d[len - 2].; all[p in d] in_svg_plane(p).

double Geom::decimal_round	(	double const	x,
		int const	places
	)

inline

Returns x rounded to the nearest places decimal places.

Implemented in terms of round, i.e. we make no guarantees as to what happens if x is half way between two rounded numbers.

Note: places is the number of decimal places without using scientific (e) notation, not the number of significant figures. This function may not be suitable for values of x whose magnitude is so far from 1 that one would want to use scientific (e) notation.

places may be negative: e.g. places = -2 means rounding to a multiple of .01

Coord Geom::distance	(	Point const &	a,
		Point const &	b
	)

inline

compute the euclidean distance between points a and b. TODO: hypot safer/faster?

Coord Geom::distanceSq	(	Point const &	a,
		Point const &	b
	)

inline

compute the square of the distance between points a and b.

Coord Geom::dot	(	Point const &	a,
		Point const &	b
	)

inline

compute the dot product (inner product) between the vectors a and b.

Matrix Geom::elliptic_quadratic_form ( Matrix const & m )

Given a matrix m such that unit_circle = m*x, this returns the quadratic form x*A*x = 1.

Matrix Geom::from_basis	(	Point const	x_basis,
		Point const	y_basis,
		Point const	offset
	)

Creates a Matrix given an axis and origin point. The axis is represented as two vectors, which represent skew, rotation, and scaling in two dimensions. from_basis(Point(1, 0), Point(0, 1), Point(0, 0)) would return the identity matrix.

Parameters

x_basis	the vector for the x-axis.
y_basis	the vector for the y-axis.
offset	the translation applied by the matrix.

Returns: The new Matrix.

ConvexHull Geom::graham_merge	(	ConvexHull	a,
		ConvexHull	b
	)

if we modified graham scan to work top to bottom as proposed in lect754.pdf we could replace the angle sort with a simple merge sort type algorithm. furthermore, we could do the graham scan online, avoiding a bunch of memory copies. That would probably be linear. – njh

Matrix Geom::identity ( )

inline

Returns the Identity Matrix.

bool Geom::is_zero ( Point const & p )

Returns true iff p is a zero vector, i.e. Point(0, 0).

(NaN is considered non-zero.)

Coord Geom::L1 ( Point const & p )

Compute the L1 norm, or manhattan distance, of p.

Coord Geom::L2 ( Point const & p )

inline

Compute the L2, or euclidean, norm of p.

Coord Geom::L2sq ( Point const & p )

inline

Compute the square of L2 norm of p. Warning: this can overflow where L2 won't.

Point Geom::lerp	(	double const	t,
		Point const	a,
		Point const	b
	)

inline

Given two points and a parameter t [0, 1], return a point proportionally from a to b by t. Akin to 1 degree bezier.

IntersectorKind Geom::line_intersection	(	Geom::Point const &	n0,
		double const	d0,
		Geom::Point const &	n1,
		double const	d1,
		Geom::Point &	result
	)

Finds the intersection of the two (infinite) lines defined by the points p such that dot(n0, p) == d0 and dot(n1, p) == d1.

If the two lines intersect, then result becomes their point of intersection; otherwise, result remains unchanged.

This function finds the intersection of the two lines (infinite) defined by n0.X = d0 and x1.X = d1. The algorithm is as follows: To compute the intersection point use kramer's rule:

* convert lines to form
* ax + by = c
* dx + ey = f
*
* (
*  e.g. a = (x2 - x1), b = (y2 - y1), c = (x2 - x1)*x1 + (y2 - y1)*y1
* )
*
* In our case we use:
*   a = n0.x     d = n1.x
*   b = n0.y     e = n1.y
*   c = d0        f = d1
*
* so:
*
* adx + bdy = cd
* adx + aey = af
*
* bdy - aey = cd - af
* (bd - ae)y = cd - af
*
* y = (cd - af)/(bd - ae)
*
* repeat for x and you get:
*
* x = (fb - ce)/(bd - ae)

If the denominator (bd-ae) is 0 then the lines are parallel, if the numerators are then 0 then the lines coincide.

Todo:: Why not use existing but outcommented code below (HAVE_NEW_INTERSECTOR_CODE)?

IntersectorKind Geom::line_twopoint_intersect	(	Geom::Point const &	p00,
		Geom::Point const &	p01,
		Geom::Point const &	p10,
		Geom::Point const &	p11,
		Geom::Point &	result
	)

Determine whether & where two line segments intersect.

If the two segments don't intersect, then result remains unchanged.

Precondition: neither segment is zero-length; i.e. p00 != p01 and p10 != p11.

double Geom::LInfty ( Point const & p )

Compute the L infinity, or maximum, norm of p.

std::ostream& Geom::operator<<	(	std::ostream &	out_file,
		const Geom::Matrix &	m
	)

inline

A function to print out the Matrix (for debugging)

std::ostream& Geom::operator<<	(	std::ostream &	out_file,
		const Geom::Point &	in_pnt
	)

inline

A function to print out the Point. It just prints out the coords on the given output stream

bool Geom::operator<=	(	Point const &	a,
		Point const &	b
	)

inline

This is a lexicographical ordering for points. It is remarkably useful for sweepline algorithms

Point Geom::operator^	(	Point const &	a,
		Point const &	b
	)

inline

This is a rotation (sort of).

template<typename T >

Piecewise<T> Geom::partition	(	const Piecewise< T > &	pw,
		std::vector< double > const &	c
	)

Piecewise<T> partition(const Piecewise<T> &pw, std::vector<double> const &c); Further subdivides the Piecewise<T> such that there is a cut at every value in c. Precondition: c sorted lower to higher.

//Given Piecewise<T> a and b: Piecewise<T> ac = a.partition(b.cuts); Piecewise<T> bc = b.partition(a.cuts); //ac.cuts should be equivalent to bc.cuts

template<typename T >

Piecewise<T> Geom::portion	(	const Piecewise< T > &	pw,
		double	from,
		double	to
	)

Piecewise<T> portion(const Piecewise<T> &pw, double from, double to); Returns a Piecewise<T> with a defined domain of [min(from, to), max(from, to)].

Point Geom::rot90 ( Point const & p )

inline

Returns p * Geom::rotate_degrees(90), but more efficient.

Angle direction in Inkscape code: If you use the traditional mathematics convention that y increases upwards, then positive angles are anticlockwise as per the mathematics convention. If you take the common non-mathematical convention that y increases downwards, then positive angles are clockwise, as is common outside of mathematics.

There is no rot_neg90 function: use -rot90(p) instead.

double Geom::round ( double const x )

inline

Returns x rounded to the nearest integer. It is unspecified what happens if x is half way between two integers: we may in future use rint/round on platforms that have them.

IntersectorKind Geom::segment_intersect	(	Geom::Point const &	p00,
		Geom::Point const &	p01,
		Geom::Point const &	p10,
		Geom::Point const &	p11,
		Geom::Point &	result
	)

Determine whether & where two line segments intersect.

If the two segments don't intersect, then result remains unchanged.

Precondition: neither segment is zero-length; i.e. p00 != p01 and p10 != p11.

template<class T >

int Geom::sgn ( const T & x )

inline

Sign function - indicates the sign of a numeric type. -1 indicates negative, 1 indicates positive, and 0 indicates, well, 0. Mathsy people will know this is basically the derivative of abs, except for the fact that it is defined on 0.

Point Geom::unit_vector ( Point const & a )

Returns a version of a scaled to be a unit vector (within rounding error).

The current version tries to handle infinite coordinates gracefully, but it's not clear that any callers need that.

Precondition: a != Point(0, 0).; Neither coordinate is NaN.

Postcondition: L2(ret) very near 1.0.

Classes

Typedefs

Enumerations

Functions

Variables

Detailed Description

Typedef Documentation

Function Documentation